Almost all class teachers or private math tutors start the circle’s topic with the story of circular shape technological invention. Do you know this? It was the wheel, Potter’s invention, in 3500 BC. It was when people began to study circles, use circular-shaped objects, and start finding their measurements using circumference, diameter, and radius.
So, let’s study the radius of a circle and how to calculate it using different methods and formulas.
In geometry, by definition, a line segment from the midpoint or center of a circle to the outer edge or boundary of the circle. It is also known as half of the length of the diameter. We use the word ‘radii’ when more than one radius is represented as it is the plural of radius.
The radius of a circle is usually represented by ‘R,’ or ‘r.’ Radius is also the dimension for a semi-sphere, sphere, cones, and cylinders with circular bases.
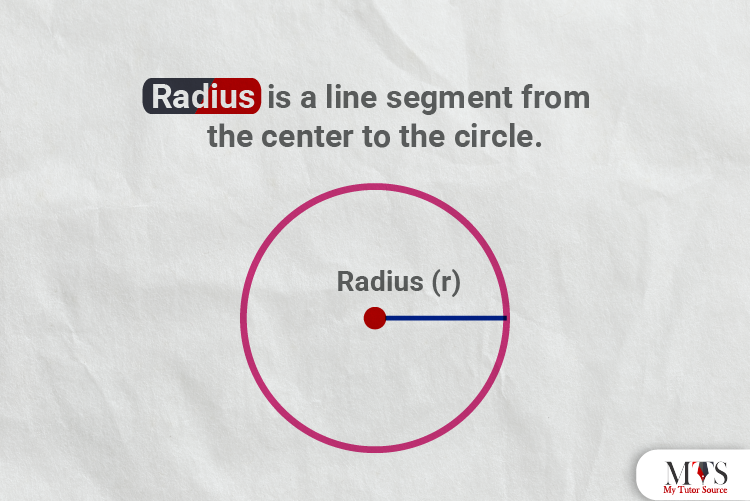
As we know, the radius is half of the diameter of a circle therefore it is formula is:
To master calculating the radius of the circle, you should know the following terms and their measurements because without using them, you cannot find radii.
The space occupied by the circle in a 2D or two-dimensional plane is known as the area of the circle. In other words, the area of any circle is the space occupied within its circumference or boundary.
It is denoted by A, and the square unit is the unit of area. For instance, m2, cm2, in2, etc.
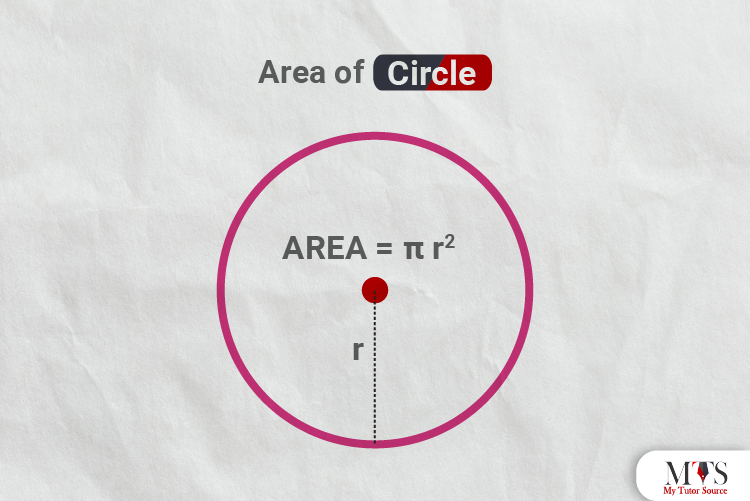
The area of a circle is calculated by
Area = A = πr2
Or,
Area = A = πd2/4
(Value of Pi = π = 3.14 or 22/7)
Formula of Area and Central Angle of a Sector
The exact central point of the circle equidistant from the points on edge is known as the midpoint or center of the circle.

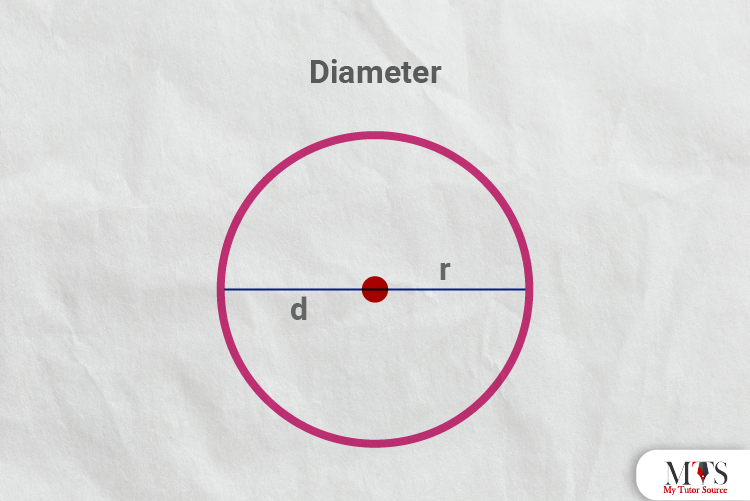
A line segment starting from one point of the circle to another point is known as the diameter of the circle. It is the longest chord that passes through the center of the circle, twice the length of the circle’s radius.
The circle’s diameter is usually denoted by ‘D’ or ‘d’. You can find the circumference of a circle and area with respect to the diameter.
The length of the circle’s boundary is equal to the circumference of the circle. Alternatively, the circle’s circumference is the perimeter of a circle.
It is denoted by the uppercase letter ‘C.’
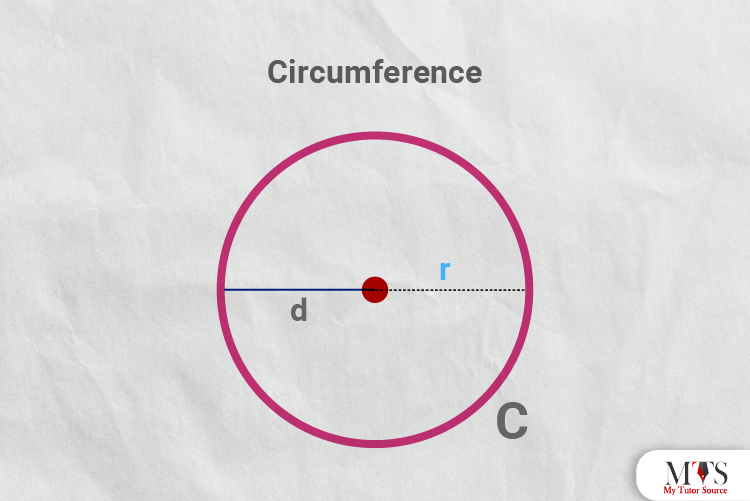
Following is the circle’s circumference formula
Circumference = C = π × d
Or
Circumference = C = 2 x r x π
You can calculate the radius of the circle by using some specific formulas. Below we have mentioned the radius formulas:
The area is the total space occupied by the circle, and the radius can be calculated using its formula.
As the area of circle = πr2
Therefore, the radius formula using the area of a circle would be expressed as:
The longest chord or a line segment twice the length of the radius is known as the diameter of a circle. With the diameter of a circle, you can easily find out the radius of the circle. Here is how:
As Diameter = D = 2 x radius
Therefore,
A circle’s circumference is known as its perimeter or boundary. This is how you can express the radius formula using the circumference of the circle’s formula:
As,
Circumference = C = 2 π r
Therefore,
In this section, you will learn how to calculate the radius of a circle by using the following formulas and practice examples in all possible four ways.
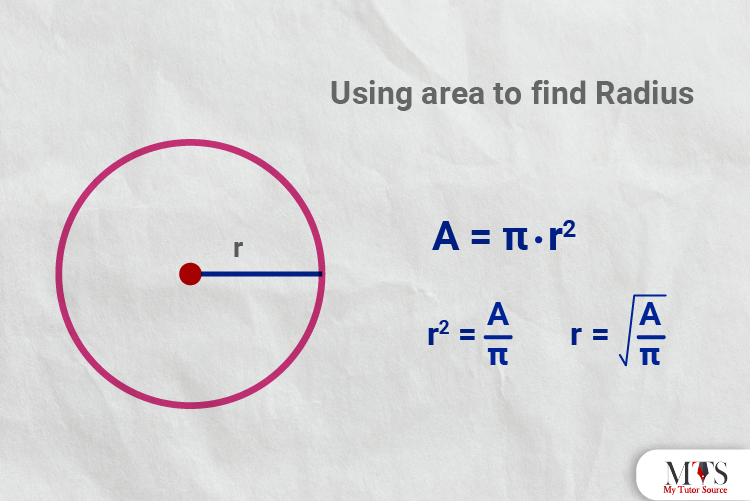
Set up the formula of the area of a circle before solving a question.
A = πr2
Therefore,
r2 = A / π
Take sqrt of both sides
⇒ r = √ A / π
If the Area of the circle is 153. 85 m2, then calculate its radius.
Solution:
As A = πr2
Given that,
A = 153. 85 m2
Pi = 3.14
Therefore,
r = √ A / π
putting values
⇒ r = √ 153.85 / 3.14
⇒ r = √ 49
⇒ r = 7
Hence, radius of the circle is 7 meters
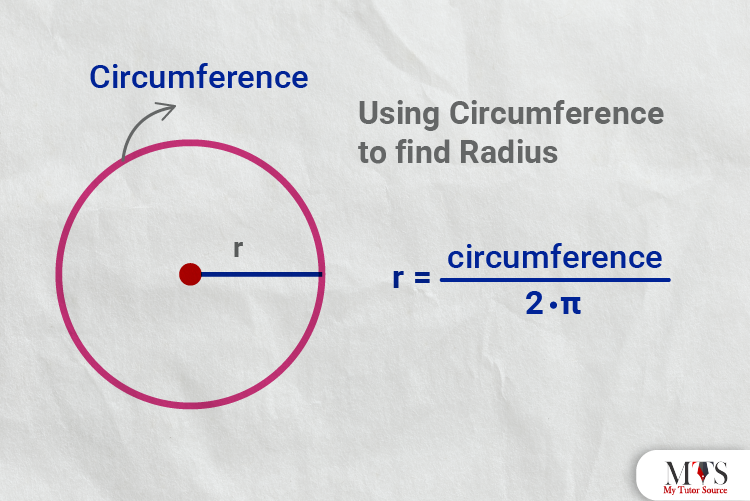
Set up the formula of the circumference of the circle before solving a question.
As
C = 2 π r
Therefore,
⇒ r = C / 2 π
Calculate the radius of the circle with 15 cm circumference. Write the complete formula.
Solution:
The formula of radius derived from the circumference of a circle formula:
r = C / 2 π
given values
C = 15 cm
Pi = 3.14
Putting values in formula
⇒ r = 15 / 2 x 3.14
⇒ r = 15 / 6.28
⇒ r = 2.39
Hence, the radius of the given circle is 2.39 cm.
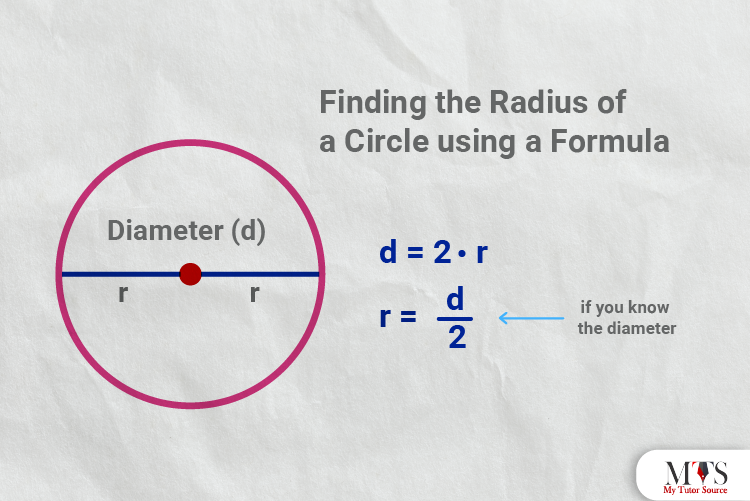
Set up the formula of the circle’s diameter before solving a question.
As
D = 2 x r
Therefore,
⇒ r = D / 2
Find radius of the circle if its diameter is 6 centimeters.
Solution:
Given that
Diameter of the circle = D = 6 cm
Using formula
⇒ r = D / 2
⇒ r = 6 / 2
⇒ r = 3
Hence, the radius of the circle is 3 cm.
Put given values in the formula of the area and central angle of a sector or A sector and after calculating all the parts step by step, take the square root of both sides to find the radius of the given circle. The formula of A sector is given below:
⇒ A sector = (θ/360°) × πr2
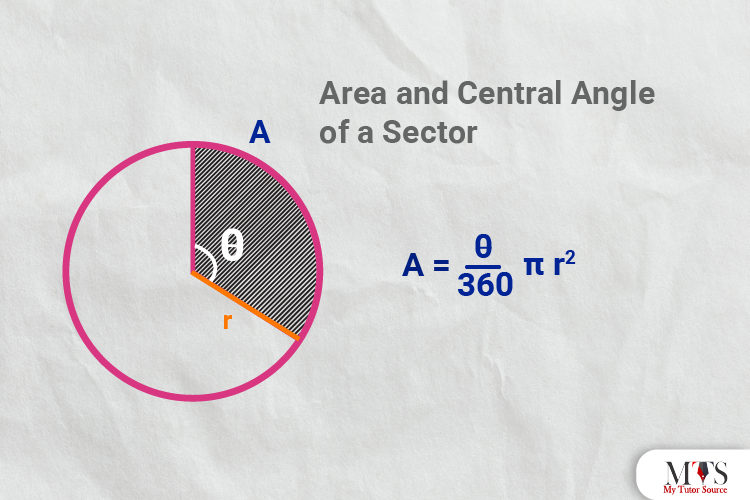
Calculate the radius if the central angle of a circle is 120 degrees with 100 cm2 area of the sector.
Solution:
Given that,
Area of sector = A sector = 100 cm2
Central angle of a circle = θ = 120°
Pi = π = 3.14
Using formula,
A sector = (θ/360°) × πr2
Putting values
⇒ 100 = (120 / 360) × πr2
⇒ 100 = 0.33 x πr2
⇒ 100 / 0.33 = πr2
⇒ 303.03 = πr2
⇒ 303.03 = (3.14) r2
⇒ 303.03 / 3.14 = r2
⇒ 96.51 = r2
Taking square root on both sides
⇒ √96.51 = √r2
⇒ 9.82 = r
Hence, the radius of the circle is about 9.82 cm.
Answer: Half the diameter of a circle is known as Radius. To summarize, a line segment joining the center to the edge of the circle is called the radius of the circle. Half the length of the diameter, easy to drill it into your mind.
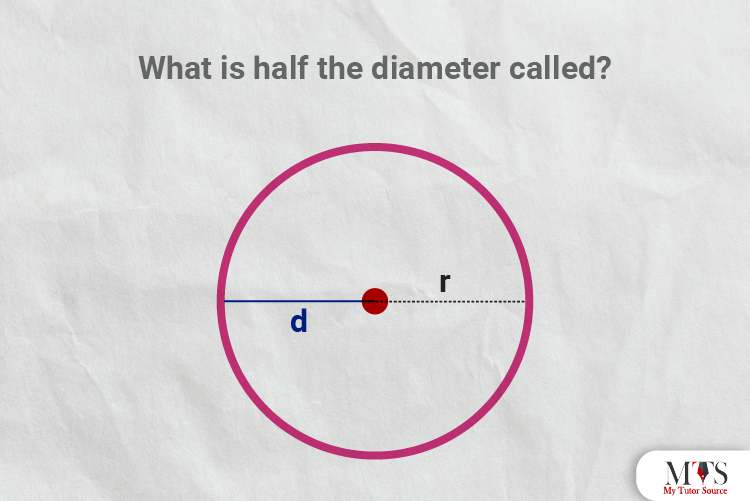
Answer: The diameter splits the circle in half, and as you know, the radius of the circle is half of the diameter. Therefore, you can easily calculate the radius of a circle through its diameter. Here is how:
Formula of diameter of circle = D = 2 x radius
Thus,
Radius = D / 2
Answer: Yes, look around, and you will see trillions of real-life examples of circles and applications of circumference. Sometimes to pick the right size of an object, we should know the distance around something, for instance, to find the right wheel for your vehicle. Moreover, to estimate the wood in a tree, measuring its circumference is easier and quicker than directly measuring the diameter. If you keep an eye, the list of examples and usage of circumference in everyday life would be endless.
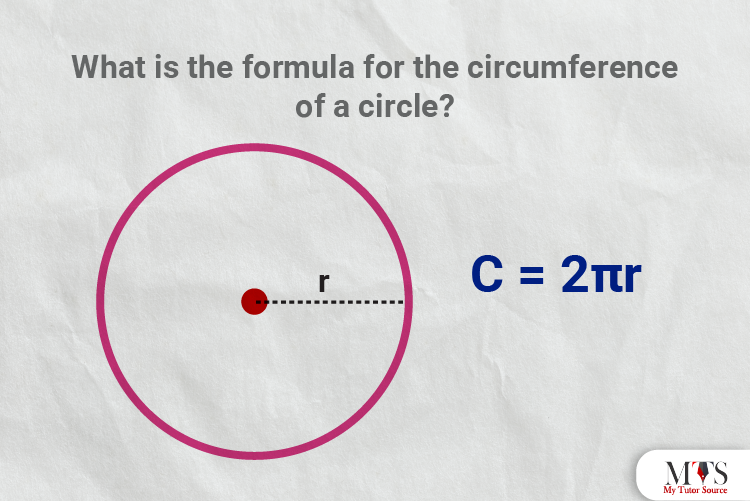
Answer: The path or boundary that defines or surrounds the shape is called the circumference of the circle. It is also known as the perimeter of the circle as it helps to identify the length of any shape’s outline.
Therefore, the formula of circumference = 2πr
Answer: A straight line joining two points on the circle is called a chord, and the longest possible line that passes through the center of the circle or twice the radius is called its diameter. However, the diameter is an example of a chord.
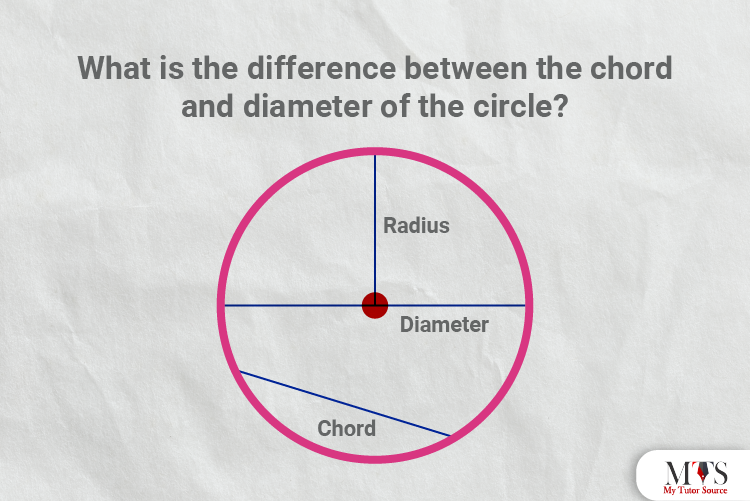
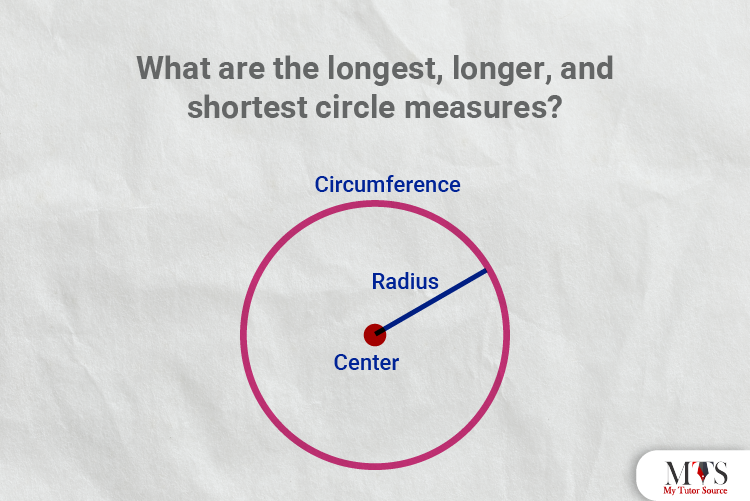
Answer: Following are the longest, longer and shortest measure of a circle:
Circumference = longest
Diameter= longer
Radius= shortest