Volume of a Cone – Definition, Formula, Derivation & Practice Questions

A three-dimensional shape with a flat base, usually a circular base, is known as a cone in geometry. In other words, the cone is a pyramid with a circular base. Cones are formed using a set of line or line segments connecting the apex or vertex (common points) with a circular base. We have common examples of cones around us in everyday life, such as funnels, Christmas trees, ice-cream cones, pencil or pen tips, castle turrets, megaphones, etc.

In this article, we will learn more about the cone, the volume of a cone with its formula, derivation, and example questions.

Definition: Volume of Cone

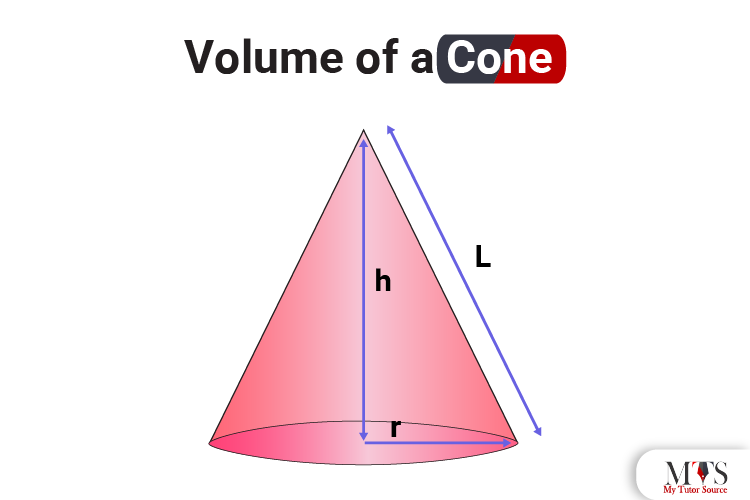
By definition, the volume of the cone is the amount of capacity or space occupied by a cone in a 3D or three-dimensional plane. The cone has a circular base made of radius and diameter, and its topmost part is measured as its height. It is further classified into an oblique cone and a right circular cone.

• A cone with a vertex above the center of the base is known as a right circular cone.
• A cone that leans over and its apex is not centered over the base is known as an oblique cone.

However, the formula for the volume of the right circular cone, regular cone, and oblique cone is always the same. Furthermore, the cubic units are used to measure the volume of cones such as m3, cm3, in3, etc.

Formula For the Volume of Cone

The cone has a circular base and a single vertex. Therefore, with the height or slant height and radius of the cone, you can easily calculate the volume of the cone. Here is the formula to find out the volume of a cone:

Volume = V = (1/3) πr2h cubic units

Where,

⇒ r is the base radius of the cone
⇒ h is the height of the cone
⇒ L is the slant height of the cone
⇒ π is equal to 3.14
⇒ 1/3 is capacity of cylinder that fits inside the cone

Volume Of Cone Formula: Height and Radius

With measures of height and base radius, use the following formula to find the volume of a cone:

Volume = V = (1/3) πr2h cubic units

Volume Of Cone Formula: Height and Diameter

We use the following formula to calculate the volume of a cone when we have the measurements of its height and base diameter:

Volume = V = (1/12) πd2h cubic units

Volume Of Cone Formula: Slant Height

To find the relation between slant height and volume of the cone, we must apply the Pythagoras theorem to the cone.

According to Pythagoras theorem,

h2 + r2 = L2

thus,

⇒ h = √ (L2 – r2)

where,

• h = height of the cone
• r = radius of the base of cone
• L = slant height of the cone

Therefore, in terms of slant height, the volume of cone will be given as:

Volume = V = (1/3) πr2√ (L2 – r2)

How Volume of Cone Formula Was Derived?

Here is an activity to show you how the volume formula was derived or obtained from the volume of a cylinder. Let us go through the activity and details:

Take one cylinder and three cones of the same height and base radius. Fill all three cones with water. Start adding water from the cone in the cylindrical container one by one. Empty one cone at one time and observe there’s still some vacant space left in the cylinder. After pouring water from all three cones in the cylinder, you will notice that now the cylinder or container is completely filled. This shows the volume of a cone is equal to 1/3 or one-third of the volume of the cylinder having the same height and base radius. Therefore, one-third of the product of the circular base area and the cone’s height is equal to the volume. Mathematically, it is written as:

⇒ V = 1/3 x Area of circular base x Height of cone
According to the formula of area of a circle, the circular base of the cone is equal to:

⇒ Area = πr2

By putting the value of area in volume formula, we get:

⇒ V = 1/3 x πr2 x h

Here we know, h is the height, r is the radius, and it is measured in cubic units.

Steps To Find the Volume of Cone

Given are a few steps or parameters to calculate the volume of the cone by using a formula.

Note: follow the given steps only when you know the base diameter, height, base radius and slant height of the cone.

1. Write down the parameters given in the question, such as r, h, d, L as radius, height, diameter, and slant height of the cone, respectively.
2. Apply the formula that matches the requirements, for instance,
   • Using base radius ⇒ V = (1/3) πr2h
   • Using base diameter ⇒ V = (1/12) πd2h
   • Using slant height and radius ⇒ V= (1/3) πr2 √ (L2 – r2)
   • Using slant height and diameter ⇒ V = (1/12) πd2√ (L2 – r2)
3. Always express the answer in cubic units.

Practice Questions

In this section of the article, we have given a few examples with their solution to help you understand the concepts of the formula of cone’s volume much better. To learn more and at your pace, we recommend you book a session with an online or private math tutor now!

Example Question: What would be the volume of the cone? If its height and radius are 10 centimeters and 5 centimeters, respectively.

Solution:

Given that,
Radius = r = 5 cm
Height = h = 10 cm
By applying formula

V = (1/3) πr2h

Putting values in the formula

⇒ V = (1/3) x 3.14 x 52 x 10

⇒ V = 262

Hence, the volume of the cone will be 262 cm3.

Example Question: Mack has an artificial ice cream cone. The diameter of the cone is 7 in with 12 in height. Find out the volume of Mack’s ice cream cone. (Use π = 22/7 or 3.14)

Solution:

Given that,

Diameter = D = 7 in
Height = h = 12 in
π = 22/7 = 3.14
As we know,
⇒ r = D/2 = 7/2

By applying formula

V = (1/3) πr2h

⇒ V = (1/3) π (D/2)2 h

Putting values in the formula

⇒ V = (1/3) × (22/7) × (7/2)2 × (12)

⇒ V = 154

Hence, the volume of Mack’s ice cream cone is 154 in3.