
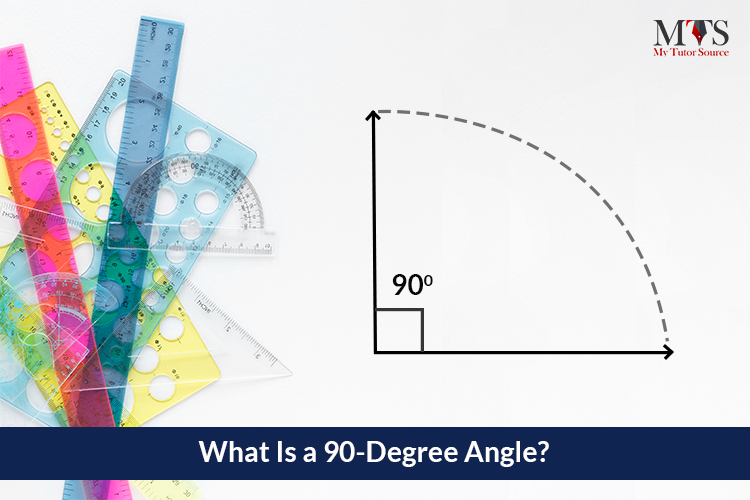
Measuring degrees of different angles with a protractor is the most straightforward and exciting activity during geometry class. To master your skills in measuring angles, let’s start from the right angle.
A 90-Degree angle is a right angle, or a 90-Degree angle is known as a right angle. You can understand it either way.
All angles are named or defined by their angle measurements, and a degree is how we measure them. In trigonometry, each angle or triangle name and degree vary; however, the degrees of a full circle of rotation is always 360.
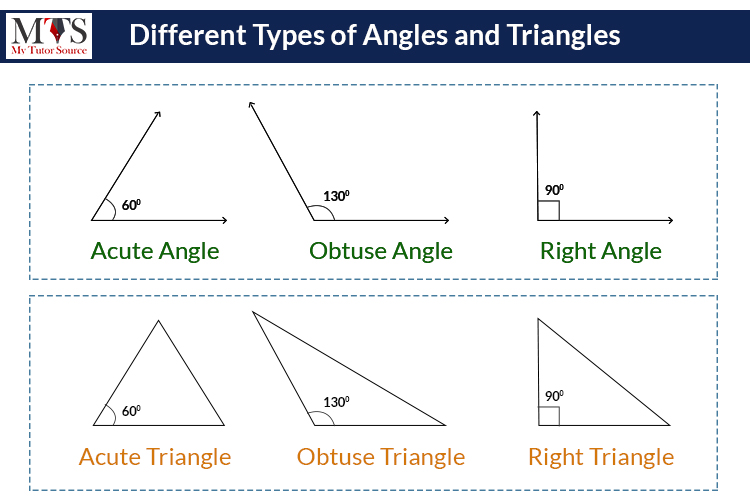
Following are the angles:
Following are the triangles:
Right-angle triangles have a few properties, and the Pythagorean theorem is used to calculate one side of a right-angled triangle. Pythagoras has discovered this theorem, and he proved that the square of the hypotenuse of a right triangle is equal to the sum of squares of the other two sides.
Note: The Pythagorean theorem cannot be applied to any triangle that does not contain a 90-degree angle.
Perpendicular lines make a perfect 90-degree angle. Two straight lines which intersect at 90 degrees are known as perpendicular lines, and they are used to measure angles and vertices in geometry. Moreover, perpendicular lines are used in daily life activities to ensure alignment in areas and straightness, like designing road maps or buildings or painting.
Radians are also used to measure the angles of triangles in geometry. The units of Radians are pi (π). The value of pi is 180 degrees, and the sum of two pi makes a 360 degrees angle. Therefore, π/2 is used to measure the radians of the right-angle triangle.
Radians are more likely to be used while working with trigonometric functions like cosine or sin. Moreover, the usage Radians are more likely to be used while working with trigonometric functions like cosine or sin. Moreover, the usage of 90-degrees angles can be seen in everyday life objects and other practical applications. Look around, ask your math tutor, and you will find them everywhere.