
In mathematics, physics, and engineering, the centroid is one of the most important concepts or topics to understand. It is helpful to study the center of a plane figure, gravity, and moments of inertia. The centroid or geometric center always seems within the triangle. Professors and math tutors teach the uses of centroid with real-life examples. To find the center of a specific area in any field, the concept of the centroid is used. In this article, we have covered the most asked questions about the centroid of a triangle, such as its definition, properties, formulas, theorems, example questions, and other important points.
Centroid is one of the important concepts and properties of triangles. Triangle is a 2D geometric shape with three sides and three interior angles. they are classified into different types based on their angles and sides, which are:
Before understanding the concept, definition, and other properties of the centroid of a triangle, we must go through the concept of medians. First, the question that begs to be asked is, what are the medians of a triangle?
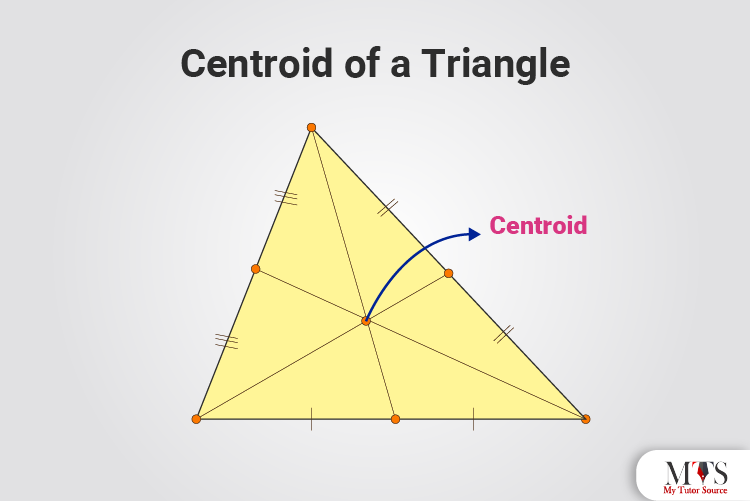
Medians of a triangle have equal areas, and each median divides the triangle into two parts or smaller triangles. Medians are the line segments drawn from the vertex of a triangle to the midpoint of the opposite side of the vertex. Here, a centroid is the point of intersection of the medians of a triangle. It is always inside the triangle.
By definition, the centroid is the center point of any object. In geometry, the point where all the three medians of a triangle intersect is known as the centroid of a triangle. In other words, you can say the centroid is the point of concurrency of all the three medians of a triangle. observe the following figure to understand the concept of centroid more clearly.
Take an average of x coordinate and y coordinate points of triangles’ all vertices to find out the centroid of the respective triangle.
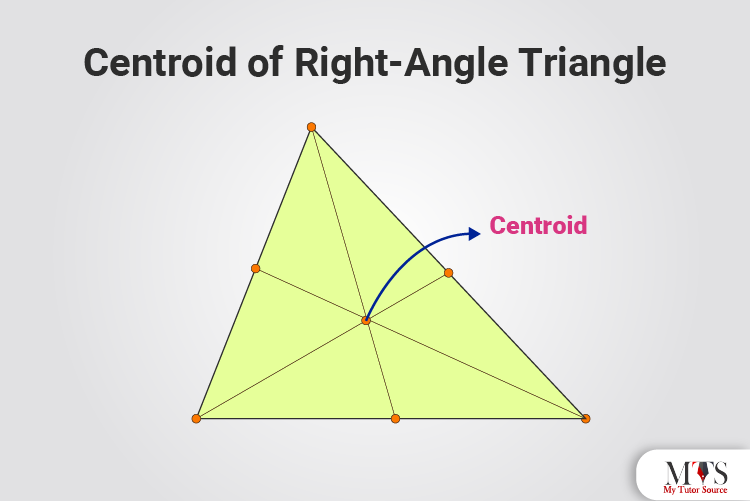
A point where three medians of a triangle intersect, drawn to the midpoints of the opposite sites from the vertices of the triangle, is known as the centroid of a right-angle triangle.
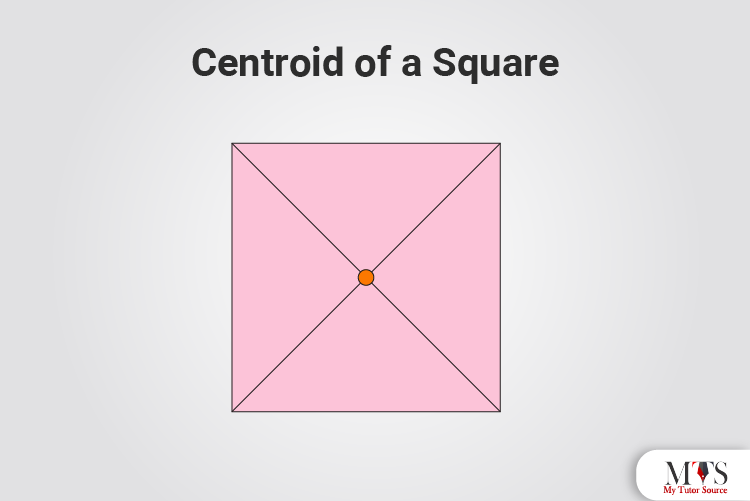
The centroid of the square is a point where the square’s diagonals intersect each other. Finding the centroid of a square is not a big deal compared to the triangle because squares have equal sides.
Centroid formula is required to determine the coordinates of the centroid of a triangle. To calculate centroid, you must find out the vertices of the given triangle. It could be any type of triangle. As triangles always have three vertices, taking the average of coordinate points is required.
Following is the formula of the centroid of the triangle:
C (x, y) = ((x1+x2+x3)/3, (y1+y2+y3)/3)
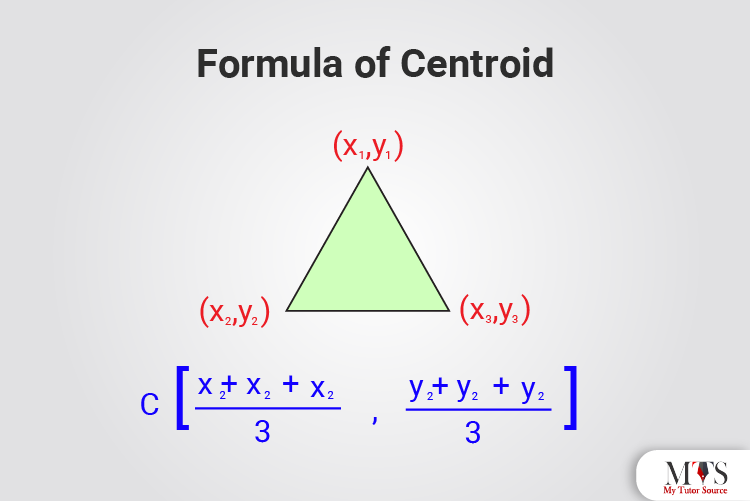
Where,
⇒ C = centroid of a triangle
⇒ x1+x2+x3 = x coordinates of triangle
⇒ y1+y2+y3 = y coordinates of triangles
The triangle’s centroid theorem states that,
The centroid is at 2/3 of the distance from each vertex of a triangle to the midpoint of the opposite side.
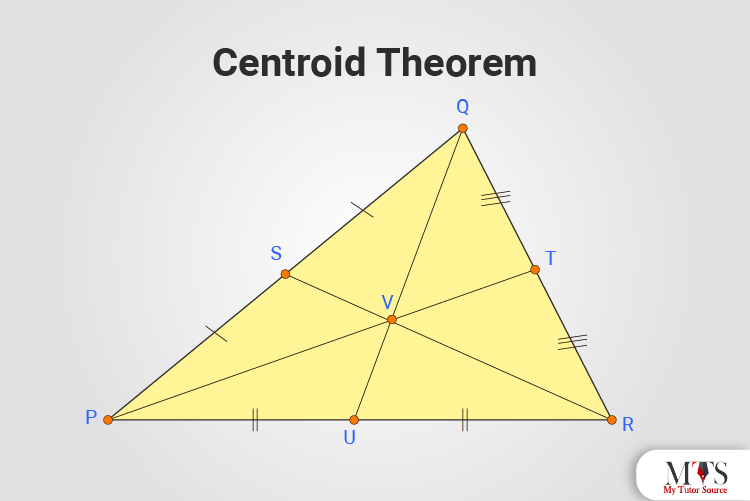
According to the image given above, V is the centroid of the PQR triangle. Where PQ, QR, and PR have the midpoints denoted as S, T, and U, respectively.
Thus,
QV = 2/3 QU,
PV = 2/3 PT and
RV = 2/3 RS
Among different points of concurrency, discovering the triangles’ centroid is a bit tricky. However, the following properties are quite helpful to distinguish it. Give them a read:
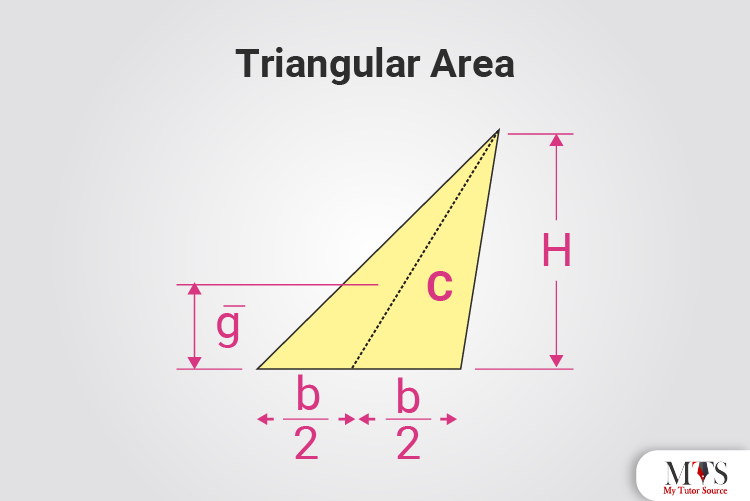
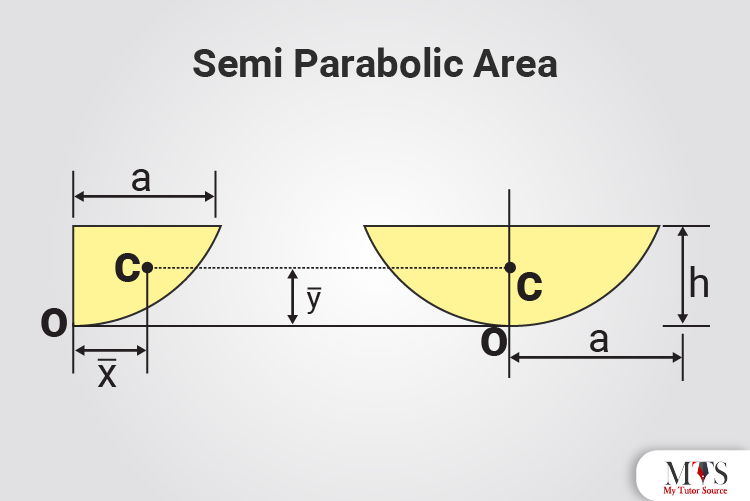
Different geometrical shapes have their centroid formula. Below are the shapes with their figure, x̄, ȳ and area
x̄ = null
ȳ = h/3
Area = bh /2
x̄ = 0
ȳ = 3h/5
Area = 4ah/3
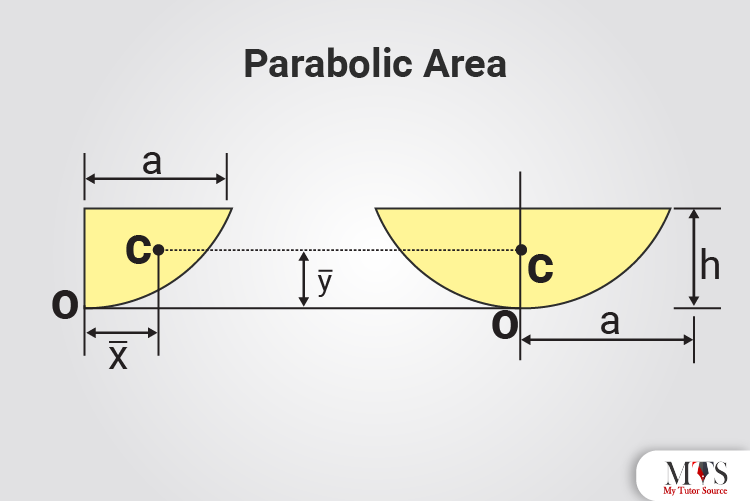
x̄ = 3a/4
ȳ = 3h/10
Area = ah/3
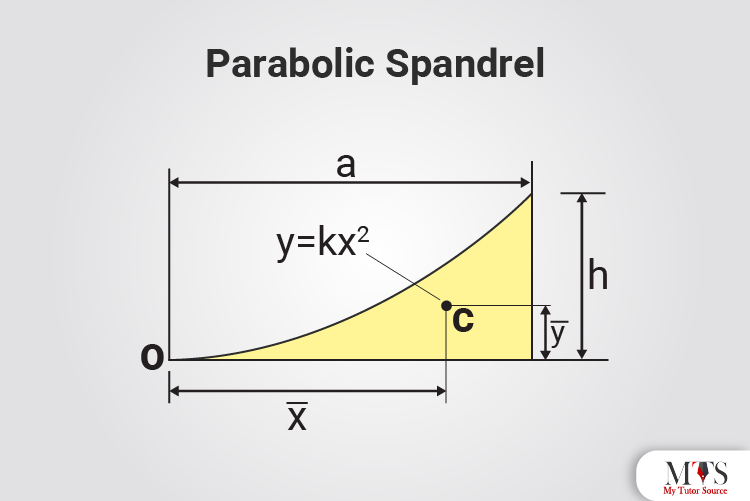
x̄ = 4r/3π
ȳ = 4r/3π
Area = πr2/4
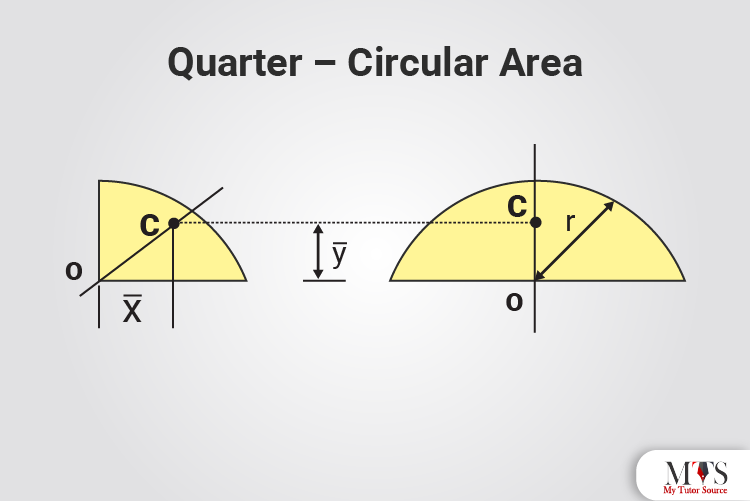
x̄ = 4a/3π
ȳ = 4b/3π
Area = πab/4
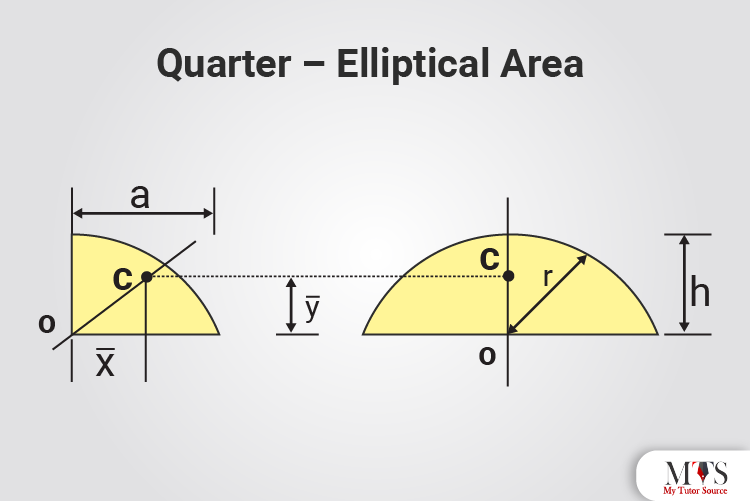
x̄ = 0
ȳ = 4r/3π
Area = πr2/2
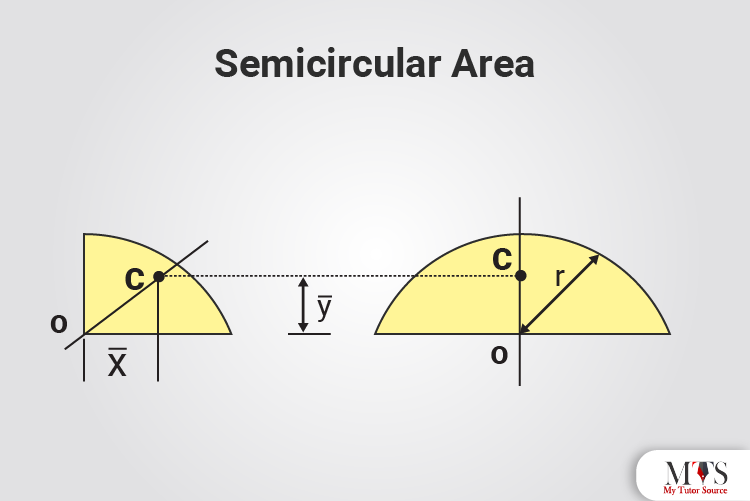
x̄ = 0
ȳ = 4b/3π
Area = πab/2
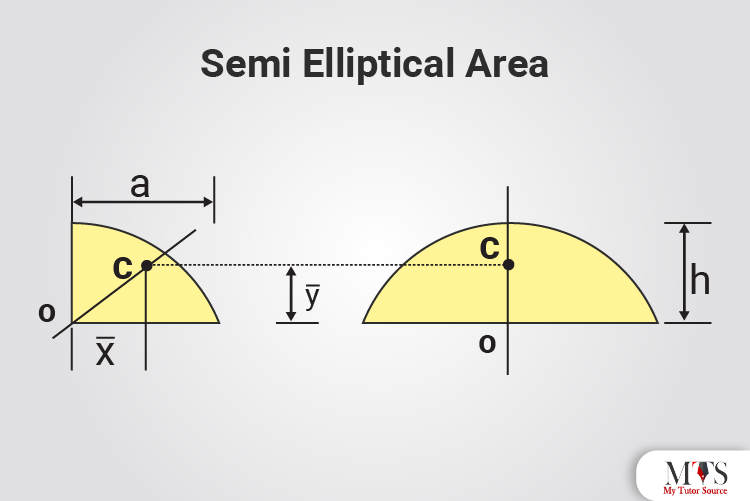
x̄ = 3a/8
ȳ = 3h/5
Area = 2ah/3
Solution:
Given that
(x1, y1) = (0,0)
(x2, y2) = (4,0)
(x3, y3) = (0,4)
As formula of centroid is
C (x, y) = ((x1+x2+x3)/3, (y1+y2+y3)/3)
By putting values, we get
C = (0+4+0)/3, (0+0+4)/3
C = (4/3, 4/3)
Hence, the centroid of the given triangle is (4/3, 4/3)
Solution:
Given vertices are
⇒ T (1, 5),
⇒ U (2, 6)
⇒ M (4, 10)
As formula of centroid is
Centroid = ((x1+x2+x3)/3, (y1+y2+y3)/3)
By putting values, we get
C = (1+2+4)/3, (5+6+10)/3
C = (7/3, 21/3)
C = (7/3,7)
Hence, the triangle with vertices T (1, 5), U (2, 6), and M (4, 10) has centroid C = (7/3,7)
The centroid is the point that lies inside a triangle where its medians intersect with each other.
The following steps are the easiest way to find a triangle’s centroid:
Centroid = C (x, y) = ((x1+x2+x3)/3, (y1+y2+y3)/3)
In the given formula, x1+x2+x3 and y1+y2+y3 are the x and y coordinates of triangles, respectively.
One of the main differences between the centroid and the incenter of the triangle are:
It lies inside the triangle.
Both incenter and centroid lie inside the triangle.
Yes, there are plenty of online centroid calculator tools. All you have to do is insert the given coordinate points of the triangle, and the tool will display the answer in a fraction of seconds.
By definition, the line segment drawn from a vertex of the triangle to the midpoint of the opposite side of the vertex is known as the median of a triangle. Medians are concurrent at a triangle point, and the concurrency point is called the triangle’s centroid.
The ratio of the centroid is formed by the intersection of the triangle’s medians. The ratio will always be 2:1 or 2/3 along any median.