Properties of Right-Angle Triangle and How to Apply Pythagorean Theorem

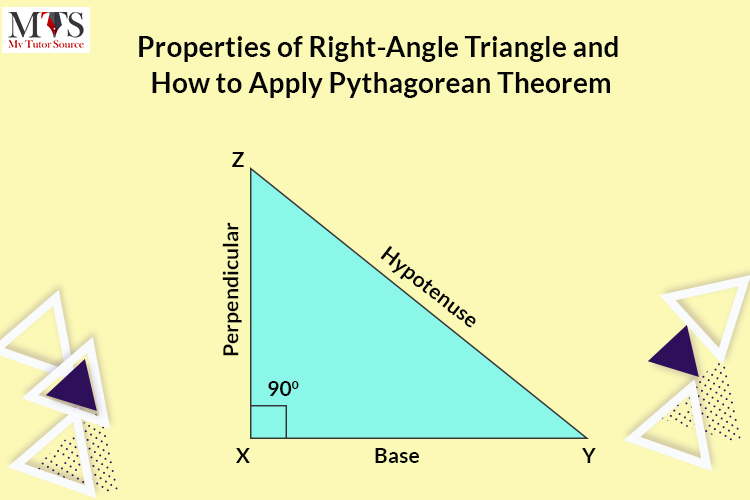
Different types of angles are used in a geometry class for measurements like acute angle, right angle, and obtuse angle. But the Right Angle is the most used in trigonometry. Let’s learn about the right angle in detail.

What is a right angle triangle?

90 degrees makes a right angle, and any triangle that contains a 90-degree angle is known as a right-angle triangle.

Different types of triangles

• An acute angle triangle has all three angles less than 90 degrees.
• An obtuse angle triangle has at least one angle more than 90 degrees.
• An isosceles triangle has two sides equivalent in length.
• In an equilateral triangle, all three sides are equal in length.
• A scalene triangle, all three sides different in length.

Properties of right-angles triangles

• One side is always 90 degrees.
• The longest side of the right-angle triangle is known as Hypotenuse.
• The other two sides of a right-angle triangle are known as base and perpendicular.
• The total sum of two sides of a right-angle triangle is always 90 degrees.
• Other than the 90 degrees side, the other two sides of the right-angle triangle are always acute angles.
• If the other two sides of a right-angle triangle are 45 degrees each, then such a triangle is known as Isosceles right-angled triangle.
• The Randian of the right-angle triangle is π/2. Pi is the unit of a radian, and it is equal to 180 degrees.
• Straight and perpendicular lines create a right angle when they intersect with each other.

Hypotenuse of a right-angled triangle

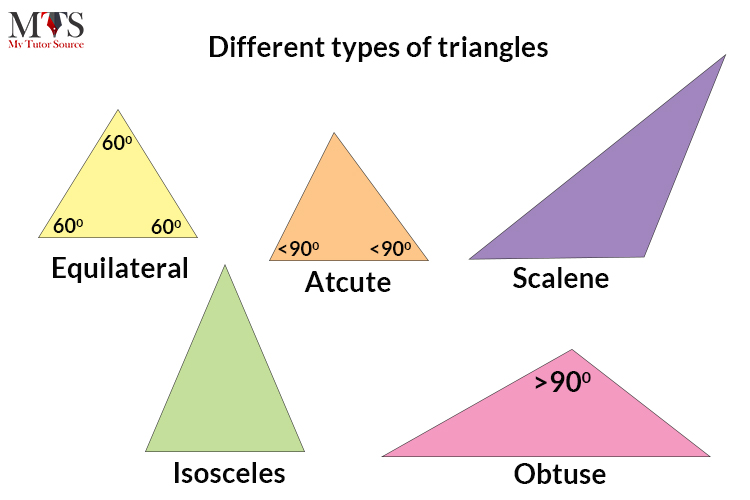
In trigonometry, most questions are on calculating the hypotenuse of a right triangle. The Pythagorean Theorem is used to find it, and high school math has such questions. Also, the converse of the Pythagorean Theorem is used to find the base of the right triangle.

If you ever get a question in an exam that asks you to calculate the hypotenuse of a triangle. For example, a triangle has two sides, a and b, and a hypotenuse c, and then you have to apply the Pythagorean Theorem to solve it.

How to apply Pythagorean Theorem

Around 500 BC, a well-known Greek Mathematician philosopher named Pythagoras developed the Pythagorean theorem.

According to the theorem, the square of the length of the hypotenuse of a right-angle triangle is always equal to the sum of the square of the other two sides of the triangle.

The Pythagorean Theorem is stated as:

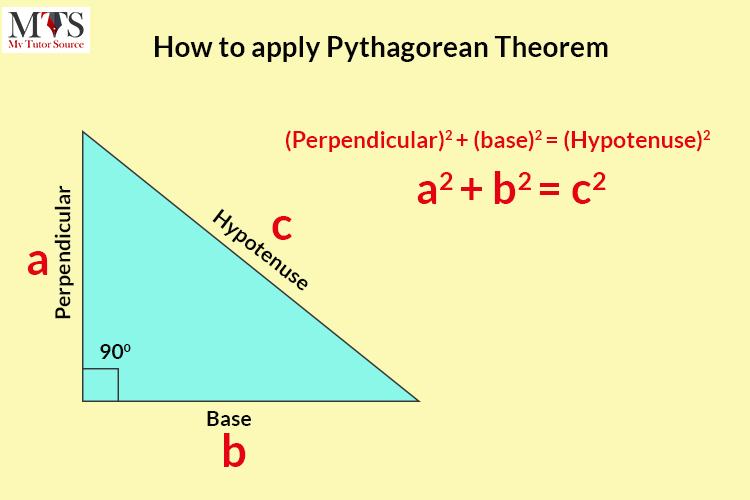
If the length of two sides of a triangle is given, we can easily find the hypotenuse length of a right-angle triangle. Let’s see an example to understand the concept of theorem better.

Question:

A triangle has three sides x, y, and z. if the length of x is 4 and y is 3, then what will the value of z? Find its hypotenuse.

Solution:

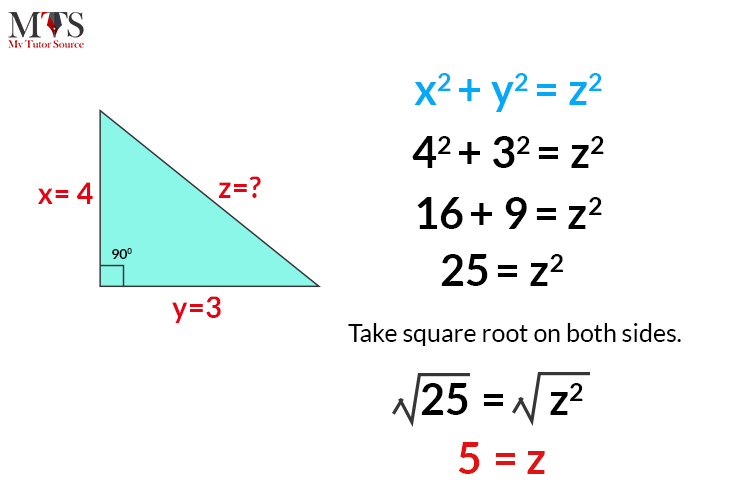
Take square root on both sides.

Hence the length of the third side of the right-angle triangle is 5.

This is how we find the Hypotenuse of the right-angle triangle using the Pythagorean theorem. If you practice enough, you can confidently apply this theorem and know how to find the third side of any triangle. However, trigonometry has more advanced functions and theorems to calculate the sides of right-angle triangles and other non-right angles.

Importance of right-angles

Right angles are used everywhere. You can easily recognize them around you in real-life objects and applications like your side table and signs on the roads. If you become an expert in applying and solving the Pythagorean theorem, you will know the importance and usage of right angles besides geometry or trigonometry.