
If a woman points toward a girl and says, “he is the daughter of my mother!” What will be the relationship between that woman and the girl? Yes, they will have the relation of sisters!
I think we all know what relation means, right? It is a connection or a link between two people or things. In simpler words, a relation defines the relationship between two. Just like this, Mathematics also has a concept of Relations that defines the relationship between two sets.
Yes… sets, relations, and functions are kind of linked with each other. Sets represent a collection of all the elements, while functions and relations define the operations performed on those sets.
What, are you getting confused? Don’t worry; as always, we are here to clear your concepts! In this article, we will elaborate on the concept of Relations in Mathematics, their use, and their types. Read on!
In Mathematics, a relation defines the connection and relationship between two or more sets of information. However, the sets must be non-empty so that their relationship can be defined.
Let’s take an example; during a school morning assembly, all the students stand in a line in ascending order according to their heights. Doing this defines the ordered relationship and connection between the students and their heights.
With that being said, we can define a relation as:
‘A set of ordered pairs is defined as a relation.’
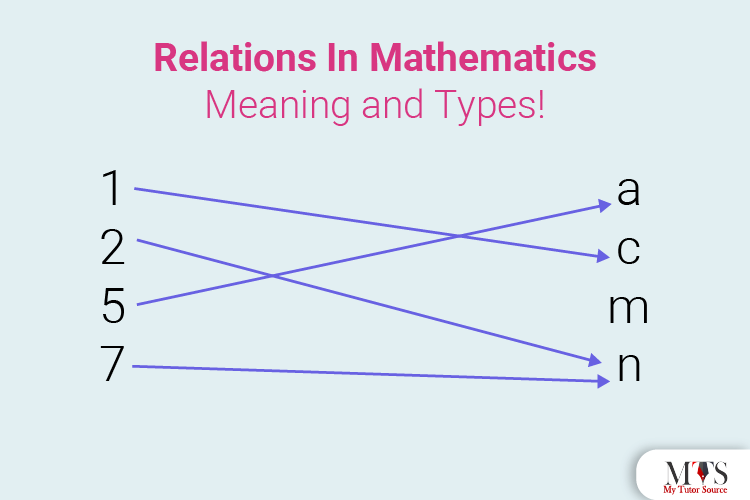
The mapping in the above image shows the relationship between Set A and Set B, and the relation from A to B will be a subset of A x B. Hence, the ordered pair we will get are:
To define this relation further, we will say:
We already know that in Mathematics, a relation is a relationship between two or more sets containing values, right? Now, let’s suppose that if x and y are two sets containing ordered pairs, and the set x has a relation with the set y. Now, the values of the set y will be called range, and the values of the set x will be called domain.
Here is an example:
Here,
Now that we have a basic understanding of Relations and how they are connected with sets, it is time to go through the different types of relations. To give you a helping hand, we are jotting down a detailed list of all the types below. Here you go:
An empty relation, also known as a void relation, happens when the elements of the two sets have no link or relation between them.
Let’s take an example for a better understanding:
If we have a set A containing 10 oranges in a basket, then we obviously won’t be able to find the relation R of getting bananas out of that basket, right? Hence, the above relation will be a void or empty relation.
A relation is known to be universal when all the elements of one set are mapped and related to all the elements of another set. Universal Relation is also known as a Full Set, and this set is the most satisfying of them all!
Here is an example for better understanding:
Suppose we have a Set P containing whole numbers, and we have another Set Q containing all integers. Then, the relation between sets P and Q will be universal, because all the elements in these sets are the same. How? Well, we know that integers are whole numbers.
If all the elements of a set are only related to itself, then it will be known as an identity relation. The identity relation is always represented by the symbol I. Here is an example for better understanding:
If we throw two dice together on a game board, we will have a total of 36 possible outcomes; 1, 1), (1, 2), …, (6, 6). If we define the relation of this set, it will be an identity relation.
A relation is called an inverse relation if a set contains elements that are inverse pairs of another set. An inverse relation is represented by the symbol R–1. Let’s take an example for a clear and better understanding:
If every element of a set are mapped to itself, then the set is known as a reflexive relation. Here is an easy example to understand the concept:
If a set A = {1,2,3}, then the relation {(1,1),(2,2),(3,3)} will be its reflexive relation. How? Because every element of a set is mapped to itself.
If the ordered and reverse ordered pair of a set are present in a relation, then it will be known as asymmetric relation. Here is an example:
If we have a ser P = {a,b}, then its relation R = {(a,b), (b,a)} will be called symmetric relation.
If (a, b) ∈ R, (b, c) ∈ R, then (a, c) ∈ R, in a set A, then the relation R will be transitive.
If a relation R is symmetric, reflexive and transitive at the same time, then it will be known as an equivalence relation.
I hope this post helped you grasping and understanding the concept of relations in Mathematics. If you still have any confusion, our professional and experienced Math tutors will help your out! So, what are you waiting for? Your tutor is just a click away. Hurry Up!
What are the types of Relations in Mathematics?
There are a total of 8 types of Relations in Mathematics; Empty Relation, Universal Relation, Identity Relation, Inverse Relation, Reflexive Relation, Symmetric Relation, Transitive Relation, and Equivalence Relation.
Can we call all functions relations?
Yes, we can call every function a relation, but we can’t call every relation a function.
What is a void relation?
Void Relation is another name for empty relation.
What is a universal relation?
A relation is known as a universal relation when every element of a set is related to each other.